Singular Terms and Reference: Evans and "Julius"
Ronald L. ChrisleyIntroduction
[1]
{S} Let us call whoever invented the zip "Julius".*With this stipulation, Gareth Evans introduced "Julius" into the language as one of a category of terms that seem to lie somewhere between definite descriptions (such as "whoever invented the zip") and proper names (such as "John", or "Julius" as usually used) (Evans 1982: 31). He dubbed these terms "descriptive names"1, and used them as a foil against which to test several theories of reference: Frege's, Russell's, and his own.
[2] I want to look at some tensions in the first two chapters
of The Varieties of Reference, tensions in Evans' account
of singular terms that become apparent his account of descriptive
names in particular. Specifically, I will concentrate on his
claim that although descriptive names are referring expressions,
they are not Russellian terms (i. e., terms which cannot
contribute to the expression of a thought when they lack a
referent).
[3] A recurring theme in this paper, and perhaps its sole
point of interest for those not directly concerned with how to
account for singular terms, is an attempt to place the blame for
Evans' difficulties with an aspect of his thinking and method
which I have referred to as "anti-realism". This might be
confusing, as the aspect I am criticising is often of a vague and
general sort, more akin to the ancient idea that "man is the
measure of all things" than to any of the technical modern
positions for which the term "anti-realism" is now normally used.
But to refer to this aspect as "Protagorean" would suggest that I
am accusing Evans of having been some kind of relativist, which I
have no wish to do. Furthermore, there are times when the aspect
does take a form which has more similarities to than
differences from conventional notions of
anti-realism.
Referring expressions and Russellian singular terms
[4] Evans claimed that both proper and descriptive names are in the same semantic category, that of referring expressions. A term is in this class if:
[its] contribution to the truth-conditions of sentences containing it is stated exclusively by means of the relation of reference.... (Evans 1982: 49; hereafter The Varieties of Reference will be referred to as VOR)It certainly seems plausible that proper names would fall into this class. Following Dummett (1973) and McDowell (1977), Evans pointed out that we can fully characterise how the name "Aphla" contributes to the truth-value of sentences in which it appears by adding the following semantic axiom to our Davidsonian truth theory (see Davidson 1967):
{1} The referent of "Aphla" = Aphlawhich "identifies the referent of a name in a way which shows or displays its sense" (VOR: 35; more on this below, in [13]). Thus, the semantic contribution of "Aphla" is stated using only the relation of reference. This is to be contrasted with, for example, predicates and quantificational expressions, which, it is at least plausible to maintain, do not refer at all, or at the very least do something else as well, so the semantic axioms used to capture their sense will have to do so using something other than the notion of reference.
[5] Evans similarly tried to show that descriptive names like "Julius" are referring expressions by constructing an axiom for the semantic value of "Julius":
(2) (x) (The referent of "Julius" = x iff x uniquely invented the zip).Evans claimed that this statement also appeals only to the relation of reference, and so "Julius" is established as a referring expression. This generalises to all descriptive names.
[6] Despite this commonality between proper and descriptive
names, Evans argued that they differ in that proper names are Russellian
singular terms, but descriptive names are not. By "Russellian singular
term", Evans means a singular term whose significance depends on its having
a referent (VOR: 46) or, equivalently, any term that, when
lacking a referent, cannot contribute to the expression of a thought
(VOR: 12).
[7] I contend that the internal tensions in Evans' position,
which arise from classifying proper and descriptive names together here,
but apart there, are intolerable, despite Evans' heroic attempts
to show the contrary. The inconsistencies appear most poignantly when he
contrasts his account of descriptive names with Russell's treatment of
definite descriptions. Seeing why requires an understanding of Evans' argument
for the Russellian status of proper names.
Why proper names are Russellian
[8] Evans' argument is from Frege. The strategy is to show that:
{E} Proper names lack sense when empty (that is, when they lack a referent).This is then supplemented with the implicit premise:
{U} There must be a unitary account of sense for both empty and non-empty cases;and one of two implicit Fregean premises:
{F1} Senses are atomic; or{E}, {U} and either {F1} or {F2} imply that a sentence containing an empty proper name lacks a complete sense, does not express a thought. Hence:
{F2} If the sense of one of the terms in a sentence is absent, then the sentence will fail to express a thought.
{C} Proper names are Russellian.
[9] The initial statement of the argument for {E} appeals to Frege's metaphorical understanding of senses as "modes of presentation":
It is really not clear how there can be a mode of presentation associated with some term when there is no object to be presented. On my interpretation of the metaphor the difficulty remains acute: it certainly does not appear that there can be a way of thinking about something unless there is something to be thought about in that way. (VOR: 22)There seem to be two ways to object to this. One, which I do not wish to pursue here, is to take an internalist line, and claim that what we might call the "factive" aspect of the notion of a mode of presentation is a superfluous part of the metaphor. One might instead think of senses as "ways of thinking which normally make possible thought about an object in a particular way", the need for some suitable cashing out of "normality" notwithstanding. If the object is not present, there might not be a factive "presentation", but there is a representation in the sense that the subject is in the same (narrow) state as they would have been if the term did refer. An obvious problem with this response is that it violates the Fregean dogma "sense determines reference". If that slogan requires that it is a necessary condition on two senses being identical that they determine the same referent, then a fortiori it requires that if one of them determines a referent, the other does also. But the internalist need not be so crude. Instead, all the internalist need do is concede that the sense of the name when it refers must be different from its sense when empty. This might seem illicit, since the whole point of the internalist move is to stress a commonality in ways of thinking when a term is and is not empty. But to do this, the internalist need not insist on identity; merely requiring the token-distinct senses to be of the same type will do all the necessary work.2 In any case, this is not an appropriate place to recapitulate the entire externalism debate, so I will move on to a second way of responding to the Fregean argument for the claim that proper names are Russellian.
[10] A second, better objection to the "mode of presentation"
argument for {E} is to claim that its scope is too broad. Evans certainly
didn't want to claim, for instance, that empty definite descriptions lack
sense. But the metaphor appears to give an elucidation of sense in general,
not just the sense of proper names. If all senses are modes of
presentation, then the sense of a definite description must be a mode of presentation
as well. But then how can one resist concluding that definite descriptions
must also be Russellian, by the same argument as the one given for proper
names? One way to resist that conclusion would be to accept that the sense
of a definite description is indeed a mode of presentation but then contend
that there is something, other than the referent of a definite description,
that is available for the definite description to present when the referent
isn't around. But this would only be of interest to someone who understands
definite descriptions as referring expressions, which Evans did not.
[11] Perhaps the metaphor "the sense of an expression is a
mode of presentation" is not meant to elucidate the sense of all expressions.
But which expressions, then? A reasonable answer would be: referring expressions
-- only through reference is something "presented" in thought, and so only
for referring expressions can there be a mode of presentation. The
problem for Evans is that this denies Russellian status to definite
descriptions, but only at the price of bestowing it on descriptive names, since Evans
has argued explicitly that they are referring expressions.
[12] The only reasonable3
option left to make the "mode of presentation" argument work seems to be
this: insist that when Frege spoke of a "mode of presentation of Meaning"
(Bedeutung), he did not just mean the special case of the Meaning
of referring expressions, but semantic values in general -- not only referents,
but reference. Then it can be suggested that definite descriptions,
along with all other expressions that have sense when they do not refer,
have as their semantic values something other than a referent, something
which they may have even when "empty" . If so, the Fregean argument
is not faulty in at least this sense: it cannot be used to establish that
definite descriptions lack sense when empty.
[13] This was Evans' position (see, for example, page 26 of VOR), and it allowed him to give a more developed explanation of why proper names lacks sense, of why {E}, and therefore {C}, is true. As mentioned briefly before, Evans accepted Frege's insight that a theory of sense should not be parallel to, but derivative from, the theory of significance of the expressions in a language. That is, the sense of a term cannot be stated, but rather it can only be shown, by stating the semantic value of a term in a way that uses the sense in question. Since the semantic value of a proper name such as "Aphla" is its referent, the sense of "Aphla" is shown by stating its referent, as in {1}, the truth theory axiom given above. The upshot:
In the event that a term appropriate for treatment in this way lacks a referent, no such clause can be truly stated, so that truth-conditions for sentences containing the term cannot be derived. (VOR: 35)When "Aphla" is empty, {1} will not show the sense by stating the referent: there is no way of showing the sense of an empty proper name. In a metaphysically anti-realist move, Evans took this impossibility of showing the sense to imply the non-existence of the sense. That is, he concluded that any term that is axiomatised in this way (i.e., any term whose semantic value just is its referent) has no sense when empty. Therefore, by the argument which was sketched at the beginning of this section, such terms would be Russellian.
[14] There is a whiff of circularity surrounding this attempt
to advert to an expression's truth theory axiom in order to
determine the Russellian status of that expression. Consider the
case of an empty "Aphla"; what is it about {1} which allows us to
conclude that "Aphla" has no sense? Is it that {1} does not
express a thought? To suppose this would be question-begging,
since what we are considering is precisely the question of
whether or not "Aphla" is Russellian -- whether or not sentences
containing it, such as {1}, can express a thought. Then the
Russellian status of "Aphla" must derive from the fact that {1}
is not "truly stated"; but doesn't treating {1} as false
contradict the idea that sentences containing "Aphla" cannot have
a truth value? Yes, but only a semantic realist is forced to
conclude the falsity of {1} from the fact that it is not true. It
is open to (even defining of) a semantic anti-realist to deny the
law of excluded middle (see also the discussion of {F2}, below).
Evans' semantic anti-realism assisted him here, but it leaves him
without a means of advancing his argument against a realist.
Also, as will be shown later, appealing to this sort of defense
will work against Evans, in that it will make it easier to show
that his establishment of descriptive names and definite
descriptions as non-Russellian is question-begging.
[15] Another concern is about the whole enterprise of
capturing the sense of names via axioms in a truth theory. The
very same name is used to denote different individuals in
different contexts (or, if one individuates names finely, the
very same marks convey different names in different contexts).
And it seems that this disambiguating context must be involved in
some way if one is to have a consistent, correct and univocal
truth theory. One could require the theorist to be in the context
which determines the usage to be that which is intended, but this
abandons any attempt at a comprehensive, context-independent
theory of meaning (in a more radical way, perhaps, than even
McDowell envisaged). One could instead try to relativise the
axioms by representing the context in them somehow. But this
would yield axioms quite different from the ones Evans
considered, and it would be unclear what impact such changes
would have on the classification of the terms they characterise
as referring or Russellian.
[16] Now we can return to the implicit premises in the
argument. To establish {C}, {E} must be supplemented by {U}, the
assumption that there must be a unitary account of sense for both
empty and non-empty cases. If {U} did not hold, then there would
be the possibility that one's theory of meaning could give a
non-unitary, disjunctive account of the sense of "Aphla" by
employing two meaning axioms, one for the non-empty cases and one
for the empty cases. Thus, the inability of {1} to show the sense
of an empty "Aphla" does not, without further qualification,
imply that an empty "Aphla" lacks sense. To make the Fregean
argument work, Evans is required to insist on unity of some sort.
This insistence may manifest itself either in the assertion that
a unitary account is desirable in its own right; or even if one
does not object to the idea of a disjunctive account in
principle, one may yet maintain that as a matter of fact, no
disjunctive account of the sense of a proper name is on the
cards. The safest choice for Evans would have been to opt for the
latter, since he was proposing a disjunctive account of a sort
(names have sense when they refer, and no sense when they do
not).4 Either
way, noting the implicit {U} premise highlights the fragility of
the streak of metaphysical anti-realism that underlies much of
Evans' thinking in this area. Crudely: if what exists depends on
what is said, then what we intuitively take to be reformulations
of the same idea will have nevertheless radically different
metaphysical implications. A realist will find the vulnerability
of Evans' account to a choice between a unitary or non-unitary
theoretical account unattractive.
[17] One might think that language is a special case in these anti-realistic considerations. That is, one might reason: of course sense isn't independent of what we say, since sense is part of an account of what we say (thanks to Tom Beament for raising this objection). Thus, sense isn't rendered less-than-real by the dependence of its existence on language any more than a mental state is rendered less-than-real by the dependence of its existence on a mental state (itself). To this I respond: of course a sense's dependence on itself doesn't imply anti-realism about sense; but if one maintains that a sense's existence depends on the properties of our theoretical account of it, then one is an anti-realist about sense. The proper analogy with mentality and objectivity is this: if a mental state's existence depends on another person's mental state (as, say, Sherlock Holmes' belief that the butler did it seems to depend on our mental states), then that mental state does not exist objectively. Evans' method of establishing singular terms as Russellian was anti-realist because it did so in a way that did make sense's existence dependent on what we can say, and not just in the trivial way that the existence of the sense depends on itself.
[18] Thus Evans' view was not that the existence of the sense of a proper name directly depends on the existence of its referent (thanks to Murali Ramachandran for this suggestion). I gather that if Evans had been confronted with a way to show the sense of a proper name without having to state the referent, then he would have accepted that empty proper names have sense. And he would have done so despite the fact that proper names are referring expressions; one only needs to look at his account to "Julius" to verify the truth of this counterfactual. No, the existence of sense, for Evans, directly depends on whether we can give an account of the sense, and it is this which I take to be an anti-realistic aspect of Evans' work.
[19] In addition to {U}, one of {F1} or {F2} is required for the Fregean argument for the Russellian status of proper names. To see why, first consider {F1}, the claim that the senses of expressions are atomistic, in that they are determined independent of context. More specifically, the assumption required is that the sense of a term is independent of the senses (and referents) of the other terms in the sentence. For suppose that this were not the case. Specifically, suppose that in the case of a proper name being empty, and therefore lacking a sense, the sense of the predicate applied to that name is different from the sense of the predicate in normal (that is, non-empty) contexts. Perhaps the sense of the (erstwhile) predicate in such a context is "saturated", a complete (false) thought. For a holist who rejects {F1} the fact that one of the terms of a sentence lacks sense (or even semantic value) does not guarantee the failure of the sentence to express a thought, at least not without further argument. Admittedly, it does seem strange to think of the sense of what we would normally label a predicate expression being an entire thought, but the example is only intended to point out the implicit premise in Evans' argument.5
[20] One could instead assume {F2}, the claim that if the sense of one of the terms in a sentence is absent, then the sentence will fail to express a thought. Evans held this, and in a robust way: if "Aphla" is empty, and thus "Aphla is white" is not true (because by {F2} it fails to express a thought at all), then so also will the sentence "It is not the case that Aphla is white" fail to express a thought (VOR: 24-25). This would block the holistic possibility just mentioned, and in a more direct way. However, there would be something perverse in Evans appealing to this Fregean premise, given some of the things he says about proper names. The Fregean argument that empty proper names lack sense presupposes a contrast between a referring name having sense, and an empty name lacking it. Yet there is a strand in Evans' work (which opposes what was said in [16]; see [24]) that rejects the notion of sense for a proper name altogether:
I remarked in 1.9 that it is not only coherent but actually quite plausible to maintain, in the case of ordinary proper names, that they are not associated with any particular way of thinking of their referents. (VOR: 69)Since, typically, sentences containing successfully referring proper names do express thoughts, then, on this Evansian hard line, it must be that proper names can contribute to the truth-conditions of sentences while simultaneously lacking any sense. But then {F2} must be rejected; of what use can it then be in establishing the Russellian status of proper names to show that they lack sense when empty?
[21] It wouldn't do to attempt a Russellian analogue of the
Fregean argument. True, equating a name's significance with its
reference would allow one to establish the Russellian status of
proper names, but that would win the battle at the price of
losing the war. Surely Evans was enough of a Fregean to want to
be able to retain the idea that "Hesperus" and "Phosphorous" make
different contributions to the meaning of a sentence, even though
they are genuinely referring expressions.
[22] Evans' flirtations with divorcing thought from language, by distinguishing what is thought from what is said, can be seen as a response to these pressures. For then one might maintain that although there is no particular sense associated with "Hesperus" in terms of what is said (no one way of thinking required in order to understand sentences containing that name), on each particular occasion of thinking a thought expressed by a sentence using the name "Hesperus", there will be some particular way of thinking of that planet. This response is more attractive once one realises that the informativeness considerations which argue against a purely referential account of the significance of proper names (that is, that it can be informative to be told that two names are co-referential) apply only within a cognitive individual. The claim that one is saying the same thing when one utters "There's Hesperus" as what is said when one utters "There's Phosphorus" is much more palatable than the claim that one is thinking the same thing when one is thinking the thoughts expressed by those two sentences (compare Carruthers 1987).
[23] Although I am in general sympathetic with attempts to
acknowledge the differences between linguistic and mental content, it isn't
something that a neo-Fregean such as Evans should enter into lightly. A
centrepiece of Frege's framework is its means of avoiding a psychologistic
view of communication, with its attendant sceptical problems, by identifying
what is understood with what is said. This linchpin will be useless if
one opens up a gap between what is understood and what is thought. Even
the revised notion of sense which Evans prefers to the "mode of presentation"
metaphor still links language and thought by seeing the senses of the former
as "ways of thinking of a referent", the province of the latter.
[24] However, we have only been examining one strand of Evans'
work. There is more reason to believe that Evans held a position that did
not require him to reject the sense of a proper name altogether, nor to
divorce language from thought: the position that proper names have sense
when they refer, and lack sense when they do not. This interpretation of
Evans' allows him to help himself to {F2}. It dovetails with the Fregean
manner of accounting for sense via sentences of the form of {1}, along
with the anti-realist assumption mentioned before: that if one cannot show
the sense for an expression, it doesn't have one. Since the sense of a
proper name can be given only when it refers, empty proper names have no
sense. This is a way of upholding the ability of referring names to participate
in thoughts, while simultaneously denying that this is possible for empty
names. Thus, Evans could still coherently argue that if a proper name lacks
sense it cannot assist in expressing a thought.
Descriptive names: The problem
[25] As has been said, Evans maintained that descriptive names are referring expressions, which means that only the relation of reference is used in a characterisation of their significance. Yet he also maintained that descriptive names were non-Russellian. These two moves seem incompatible by the following line of reasoning:
{X} Descriptive names are referring expressions -- their contribution to the truth-conditions of sentences containing them is stated exclusively by means of the relation of reference.Then the Fregean argument takes hold again, concluding, as we saw, from {Z} that descriptive names are Russellian. Another way of putting this is: the Fregean argument for the Russellian status of proper names relied only on the fact that the latter were referring expressions, whose significance was their reference. If descriptive names are in the same class, the same argument applies.
{Y} If reference is the only relation used in stating how a term contributes to the truth-conditions of sentences in which it is embedded, that term's significance just is its reference.
{Z} If a term's significance is its reference, then its significance will be absent when it is empty.
[26] Putting descriptive and proper names into the same class causes difficulties in the other direction as well. In trying to make sense of how descriptive names can have sense when empty, one must try to make sense of how a referring expression can have sense when empty. Thus Evans' discussion on page 32 of VOR:
If we wished to incorporate significant but empty Proper Names within a Fregean framework, one formally adequate possibility would be to regard the semantic value of each singular term as a set, which would be either the singleton of the referent or the empty set, according to whether or not the term has a referent. If no one person invented the zip, the name "Julius" would have a semantic value, namely the empty set, but it would have no referent.One problem is that this suggestion for making sense of descriptive names referring but being non-Russellian could also be applied to proper names themselves. Unless we are given independent grounds for assigning a set as a semantic value to descriptive names, but not to proper names, this suggestion will work against Evans as much as for him. Later, I will propose an axiomatization of proper names that gives one as much grounds for assigning a set as the semantic value for proper names as axioms like (2) do for descriptive names.
[27] Another problem is that this complication of an
expression's semantic value beyond having a referent is ipso
facto grounds for holding that an account of its contribution
to truth-conditions must involve more than the relation of
reference. One can only make the set-theoretic move to deny
the Russellian status of descriptive names at the price of also
denying their status as referring expressions.
Infinite domains
[28] I said before that the inconsistencies in Evans' position appear most poignantly when he contrasts his account of descriptive names with Russell's treatment of definite descriptions, expressions such as "the author of Waverley". Now we are in a position to look at those inconsistencies. Russell maintained, as did Evans, that the best account of definite descriptions is to treat them as quantificational, rather than as referring expressions. But Evans did not think that Russell's account had the resources with which to resist the referential view of definite descriptions, thus necessitating Evans' own account. When discussing this he says the following (VOR: 53):
Obviously, definite descriptions, if they were referring expressions, would be non-Russellian. We should not expect a semantic theory to comprise a clause for each description, of the formIf one paused there in one's reading, one might interpret this as saying: the above truth theory axiom would yield a Russellian term, and since definite descriptions, were they referring expressions, would be non-Russellian, we would not expect them to be like (13). Indeed, I myself interpreted Evans in this way in an earlier paper.6 My argument then was that if (13) implies Russellian status, then how could the axiom for "Julius" (2) fail to do likewise, given that the structure of the two is identical? But I should have known better, and the phrase "for each description" should have been my clue that Evans was only making an incidental point, a point about the number of semantic axioms. The next sentence of Evans' text confirms this interpretation:(13) (x) (the referent of "The author of Waverley" = x iff x uniquely wrote Waverley)
For there are infinitely many descriptions, and anyway we shall need to show how their reference depends upon the significance of the words embedded in the description. Rather, a theory which treated definite descriptions as referring expressions would contain a single recursive clause on these lines:Evans gave (14) as example of an axiom that, if adopted, would imply that definite descriptions were referring, yet non-Russellian expressions. However, there are some difficulties with both of these claims. Concerning the first, note that the axiom employs more than the notion of reference: it also appeals to the concept of satisfaction. To avoid attributing a blatant contradiction to Evans, one must assume that he was employing a less-than-strict understanding of what it is for a truth theory axiom to be "stated exclusively by means of the relation of reference". But then it becomes unclear what axioms, other than those which do not appeal to reference at all, he would have ruled out of this class. The theoretical interest of claiming both that descriptive names are referring and that they are non-Russellian is greatly reduced if the former claim is trivialised by a promiscuous notion of what it is to be a referring expression. Nor could Evans have escaped difficulty by accepting that the use of the notion of satisfaction in (14) renders definite descriptions non-referring.8 A hypothetical consideration will show why.(14) (x) (The referent of "The" ^f = x iff Satisfies(x,f)). *Such a theory would enable us to derive truth-conditions for any sentences containing a definite description, whether or not the description was empty. (VOR: 53).7
[29] Evans rejected (13) in favour of (14) because of the former's inability to handle the infinitely productive nature of definite descriptions.9 There would have to be an infinite number of such axioms in one's theory in order to account for the infinite number of definite descriptions one can create through composition, and no one wants an infinitely large theory.10 The problem, though, is that it seems that this same line of reasoning can be applied to descriptive names, since if the number of definite descriptions is infinite, so then is the number of potential descriptive names. This point can be made more concrete by supposing that we enumerate the definite descriptions: they are infinite in number, but denumerable. We can then construct a function D such that D(n) yields the nth definite description. Now consider the following stipulation:
{S*} Let us call whoever uniquely Satisfies D(n) "Brutus"n.11We then can construct the appropriate axiom for this family of terms:
{2*} (n)(x) (The referent of "Brutus"n = x iff Satisfies(x, D(n))).If simplicity considerations force us to abandon (13) in favour of (14), then in our attempts to construct a theory of meaning for a language for which stipulation {S*} is appropriate we should also have to abandon (2) in favour of {2*}. And if, as we are temporarily supposing, (14) implies that definite descriptions are non-referring, then we must also classify the expressions characterised by {2*} as non-referring expressions. So Evans would have had to contend that while normal descriptive names such as "Julius" are referring expressions, expressions such as "Brutus127" (which, it seems quite plausible to say, are also descriptive names) are not referring expressions. Yet it seems unsatisfactory that recursive introduction, which is the only difference between the "Brutus" series of descriptive names and "Julius", should imply a difference of semantic category. At the very least, Evans would have to concede that descriptive names as a whole are not both referring and non-Russellian; at most a subset of them are. However, I feel that the best moral we can draw from this fragility of Evans' account is to have a healthy scepticism concerning the anti-realist methodology of classifying entities (in this case, expressions as either referring or non-referring) solely according to the properties of their representation in some formalism (the meaning axioms).
Non-Russellian Names?
[30] To return to (14): Evans thought that it implied that definite descriptions are not only referring, as has just been discussed, but non-Russellian as well. There is another, potentially more serious difficulty here: if (14) is sufficient to establish the non-Russellian status of definite descriptions, then one can establish, in a similar manner, the non-Russellian status of proper names. This can either be viewed as a direct contradiction of Evans' views on proper names, or (more charitably perhaps) as a reductio ad absurdum of the idea that (14) establishes that definite descriptions are non-Russellian. Consider the recursive truth theory axiom for proper names:
{N} (A) (x) (The referent of A = x iff satisfies(x,fA))where fA is the property of being the referent of A. Clearly {N} is of the same form as (14), so if it is the form of the truth theory axiom for an expression which determines its semantic class, Evans would have to conclude that {N} establishes proper names as non-Russellian, since it would enable us to derive truth-conditions for any sentences containing a proper name, whether or not the proper name was empty (compare page 53 of VOR).
[31] Admittedly, {N} seems fishy. Perhaps it is circular? Not
in any direct sense; for example, it does not use, on the
right hand side, the name it is characterizing on the left
hand side. Even if it did, there is a long respectable history of
"circularity" in theories of meaning: witness Tarski, Davidson
and McDowell. The (nearly) pleonastic nature of {N} is no more
illicit than the disquotational elements of those accounts, nor
indeed than {1} itself. It is, in fact, the circularity of {1}
which results in it not being able to show the sense of "Aphla"
when empty, so circularity itself cannot be used by Evans as an
objection to {N}. I suspect that an instinctual opposition to
circularity of this sort derives from a latent reductionism; if
the best we can hope for is a "modest" theory of meaning, then it
is quite plausible that at least some proper names will be in the
"primitive fragment" that cannot be given a non-circular account
(see McDowell 1987). To account for such expressions, an
insistence on holding out for a less circular axiom than {N} is
misguided. Especially since {N} is not, as said before, circular
in this way. Nor in any other relevant way I can think of. For
example, an understanding of {N} or one of its instances does not
require one to already know the referent of the expression whose
reference is being stated (thanks to Murali Ramachandran for this
notion of circularity). Perhaps what was behind the charge of
circularity was a suspicion that {N} is uninformative. But
the suspicion is unfounded: even well-known truths can be
illuminating (and hence informative) if stated in the proper way.
I take it that an acknowledgement of this fact must underlie the
entire Fregean approach of showing the sense by stating the
referent in the right way.
[32] The objection might not be that {N} is circular:
I think that there is nothing wrong with {N}, but using it will not show that proper names are non-Russellian, since when the name has no reference, nothing will still be specified. This will contrast with the case of descriptive names, since the use of a predicate in the specification will give the descriptive name a COUNTERFACTUAL bearer, even if it is empty in the actual world (Michael Morris, personal communication, 2 December, 1998).There are two ways to reply to this. First, one could insist that if the use of a predicate in the meaning axiom for a descriptive name gives it a counterfactual bearer, then so also will the use of a predicate in {N} give proper names counterfactual bearers. Even if no one uniquely invented the zip, "Julius" can contribute to the thoughts we express, because we know what would have to be true for someone to satisfy the predicate "uniquely invented the zip". Similarly, even if "Aphla" is empty, it can contribute to the thoughts we express, since we know what would have to be true in order for something to satisfy the predicate "is referred to by 'Aphla'". I see no problem in grasping what would have to be true for Mount Blanc to satisfy the predicate "is referred to by 'Aphla'": it would have to be the case that "Aphla" refers to Mount Blanc. So there appears to be no difference from the case of non-Russellian descriptive names.
[33] For those who do not find that kind of response
satisfying, there is another reply to Morris. This is to deny
that the only way to establish a referring expression as
non-Russellian is by providing it with a counterfactual bearer
when empty. One is entitled to take this line against Evans or a
defender of Evans because of his treatment of the distinction
between referent and reference; for Evans, even a referring
expression may have the latter when it does not have the former,
and only the latter is required in order to show (and therefore
have) sense. "Aphla" might be said to have reference even if has
no referent (not even a counterfactual one). What could this
reference be? It must consist in the fact that it is
supposed to have a referent, that it is an empty referring
expression rather than, say, a predicate that is not understood.
Contrast "Aphla is larger than Mount Blanc" with "The man fribbed
his way through the lecture". That we appeal to the context in
which "Aphla" is used, specifically to the semantic values and
senses of the expressions around it, in order to determine, in
any given case, that the role of "Aphla" is referential does not
count against the reply I am making to Morris. Specifically, it
does not mean that I am employing a non-atomistic notion of
sense, as discussed earlier. Following Evans, the cognitive means
by which we determine the reference of "Aphla" is not relevant
here, only the account of "Aphla" in our truth theory; {N} states
the reference of "Aphla" in an atomistic way, and does so in a
way which reveals its sense. Or at least it does so to the same
extent that (14) does so for definite descriptions and (2) does
so for descriptive names.
[34] Another objection might be that the recursive, quantified
form of {N} prevents it from doing what it is meant to do: show the sense
of the proper names it is meant to characterise. I'm not so sure. We saw
that Evans pulled back from the brink of concluding that proper names lack
sense, to instead posit an unhappy dualism between language and thought.
Perhaps his arguments should be interpreted in another way: as showing
that proper names do have sense, but it is of a very thin kind, and is
shown in {N}. That is, the sense of a proper name is, roughly, the fact
that it refers (or is supposed to refer) to something.
[35] Thus, {N} cannot be rejected on grounds of ill-formedness,
uninformativeness or circularity. In fact, any such remarks tell equally
against (14): someone objecting to {N} must say why (14) doesn't fall afoul
of the same considerations.
Circularity again
[36] We saw before that using {1} to establish the Russellian
status of proper names appeared to be question-begging, because it seemed
to require one to assume that {1} could not express a thought when "Aphla"
is empty, in order to conclude that "Aphla" is Russellian. But we
also saw that there was no question-begging going on, since Evans could
rely on the fact that {1} is not true, rather than relying on it not expressing
a thought. However, using clauses such as (2) to establish the
non-Russellian status of descriptive names requires one to have established that definite
descriptions are non-Russellian, and using clauses such as (13) to
establish that is question-begging. I will argue for this
in two stages.
[37] Stage 1: Clauses such as (2) allow us, Evans claimed, to
derive truth-conditions for sentences containing "Julius" even
though "Julius" is empty. I assume that (2) can do this only if
it expresses a thought; if it fails to express a thought, then no
truth-conditions can be determined. But if "Julius" is empty,
then the definite description "The referent of 'Julius'" is
empty. Thus, (2), which uses that definite description, can only
allow us to derive truth-conditions for an empty "Julius" if
definite descriptions are non-Russellian. For if they were
Russellian, (2) would not express a thought.
[38] Stage 2: Using clauses such as (13) to establish that
definite descriptions are non-Russellian is question-begging. To
show that one can derive truth-conditions for sentences
containing "the author of Waverley", even though "the
author of Waverley" is empty, one must show that (13)
expresses a thought when "the author of Waverley" is
empty. But when that definite description is empty, the definite
description "The referent of 'the author of Waverley'" is
empty as well. Yet (13) uses the latter definite description. So
we can only show that (13) expresses a thought if we show that
"The referent of 'the author of Waverley'" is
non-Russellian. And so we have a question-begging regress: we can
use Evans' method to show that definite descriptions are
non-Russellian only if we assume that they are so in the first
place.
[39] So we are left without an argument for the non-Russellian
status of descriptive names, or even definite descriptions. But there
are three ways one might respond to the preceding argument.
[40] First, one might object that the argument confuses the object-language with the meta-language (thanks to Tom Beament for making this point). That is, we have to assume an independent meta-language within which to give an account of the object-language, and independence here means that what is said about the object-language has no implications for how we use the meta-language, and vice versa. Thus, assuming that definite descriptions of the meta-language are non-Russellian is not question-begging with respect to the Russellian status of expressions in the object-language.
[41] Surely this objection is at odds with the methodology that Evans employed in this area, which involves admitting no sharp object/meta distinction. The Fregean requirement that the sense be shown by stating the referent in the proper way demands that the meta-level have and use the expressions of the object level. Further, the whole idea of concluding that "Aphla" on the object-level is Russellian from the fact that the use of "Aphla" on the meta-level renders {1} unintelligible relies crucially on there being a dependence between the "two levels", if such can be demarcated.
[42] A second objection tries to make something of the
difference between (13) and (14). Perhaps there are difficulties
with (13), but we have already seen that Evans claimed that the
person who wishes to view definite descriptions as referring
expressions should account for them with (14) anyway, in order to
avoid an infinite number of axioms. This is fortunate, since (14)
is not vulnerable to the argument just made in the way that (13)
is. Specifically, it uses no definite descriptions of the
object-language, but rather involves a schematic variable "f" being concatenated to a string, "The".
This means that (14) always expresses a thought, no matter which
definite descriptions are empty, and thus definite descriptions
must be non-Russellian. So they can be used, when empty, to
capture the sense of descriptive names, as in (2). So descriptive
names are non-Russellian as well.
[43] The problem here is that (14) in itself does not give the
sense of any definite descriptions. It is a universally
quantified proposition the various instantiations of which
do express the senses of the corresponding definite
descriptions. And it is these clauses with various instantiations
of "f" which cannot establish definite
descriptions as non-Russellian in a non-question-begging way. It
might be thought that this stripping away of the universal
quantifier might have he same effect on {N}: it is only the
instantiations of {N} which can show sense, so the fact that {N}
always expresses a thought, even when some names it ranges over
are empty, is irrelevant. True, but notice that the
instantiations of {N} do not use any proper names either; they
only mention them. So all of them can express thoughts when the
name they are mentioning is empty, and thus {N} can be used as
intended: to establish proper names as non-Russellian.
[44] The third objection, then, is to point out that we can make the instances of (14), such as (13), more like {N}; just as the instances of {N} use no proper names, the instances of (14) should use no definite descriptions. For example, (13) can be re-written to be:
(13*) (x) (Refers("the author of Waverley", x) iff x uniquely wrote Waverley)This involves no reference to the referent of "the author of Waverley", so it does not allow for a Russellian interpretation of definite descriptions.
[45] This objection, I think, hits the mark, and if it is made, it allows
Evans' story about definite descriptions and descriptive names to go
through. But making this move of emulating {N} in order to save the non-Russellian
status of definite descriptions and descriptive names only serves to validate
{N} as an account of proper names. Thus we have once again the familiar
pattern: Evans' view on descriptive names can only be salvaged at
the price of abandoning his view of proper names, and vice versa.
[46] Thus, what Evans said about (13) and (14) creates two problems for his
story in general: it allows one to conclude that descriptive names
are non-referring, and it forces one to conclude that {N} establishes proper
names as non-Russellian. But (13) and (14) are not essential aspects
of Evans' position; indeed he rejected them and referential accounts of
definite descriptions in general. So perhaps Evans could have escaped
the two problems by taking back what he said about (13) and (14).
Perhaps they would not establish definite descriptions as referring yet
non-Russellian.
[47] This wouldn't have let Evans off the hook, for two reasons. For one thing, Evans used the relative success of (13) and (14) as a sign that Russell's own account should be rejected, since it could not give one the means of rejecting referential accounts of definite descriptions. If (13) and (14) are recognized as not delivering the goods, then Russell's account looks more attractive: Evans' alternative is not required.
[48] More relevant to the discussion at hand is to note that only the first
of the two problems can be dissolved by disowning the claims concerning
(13) and (14). Perhaps one can take {2*} to establish descriptive
names as referring expressions, despite the fact that it employs the relation
of Satisfaction. But the problems that {N} raises still remain even
when (13) and (14) are disowned.
Finite domains
[49] To close, I would like to consider a direct argument against
the claim that (2) establishes descriptive names as non-Russellian (direct
in that it, like the argument involving {N}, does not depend on inessential
aspects of Evans' theory). If the remarks at the end are correct,
then it is not entirely successful. However, I do think that considering
it further illuminates Evans' thinking on these issues.
[50] The argument is based on the similarity between (2) and {1}, which Evans takes to establish the Russellian status of a typical proper name, "Aphla". In the case of a finite domain, we can remove the quantifier in (2) by enumerating over all the individuals in the domain. Thus, for the domain {Gottlob, Bertrand, Gareth}, we would have as an axiom for "Julius" a conjunction of the form:
(2') [The referent of "Julius" = Gottlob iff Gottlob uniquely invented the zip] and [The referent of "Julius" = Bertrand iff Bertrand uniquely invented the zip] and [The referent of "Julius" = Gareth iff Gareth uniquely invented the zip].
[51] Now we can return to a question we considered earlier, namely,
can empty terms without sense contribute to a thought? Suppose that they
cannot. Then "Julius" must have a sense when empty, since Evans has argued
that "Julius" is non-Russellian (i.e., that "Julius" can contribute to
thoughts even when empty). So that means the conjunction above must display
the sense of "Julius" when "Julius" is empty, that is, when neither Gottlob,
Bertrand, nor Gareth uniquely invented the zip. In that case, there will
be no sentence that will show the sense of "Julius" by stating its reference.
But this is just the same situation as an empty proper name, only Evans
used that as evidence for the conclusion that proper names have no sense
when empty, and are therefore Russellian. It would seem strange that a
descriptive name gains sense (and therefore non-Russellian status) just
because we conjoin some sentences that individually don't express it sense.
If that were to work for a descriptive name, there is no reason to suppose
that it wouldn't for a proper name. Thus, it seems that one can only
maintain the non-Russellian status of descriptive names if one accepts
that proper names are likewise non-Russellian.
[52] But why think that we have here is a descriptive name?
It seems that it would be better to call it a disjunctive name.
So anything said about "Julius" in the case if a finite domain has nothing
to do with "Julius" in the case of an infinite domain, which does not admit
of an account along the lines of (2'), and is therefore a descriptive,
not disjunctive, name. This is an odd suggestion. Since the
statement quoted at the beginning of this paper, {S}, that introduces
"Julius" into the language is the same in both cases, the proposal must
be that the semantic classification of "Julius" as either a descriptive
or a disjunctive name depends entirely on the size of the referential
domain. Yet there seems something wrong with this: for
one thing, it would imply that the semantic class of "Julius" is entirely
external to us: it would be an empirical, even scientific endeavour
to determine whether "Julius" is Russellian or not. But don't all
natural language expressions ranging over past persons actually have a
finite referential domain? I suppose some might wish to deny this, and
appeal to an idea of an infinite universe, the possibility of fictional
referents, or some such. I think that any theory of reference that has
to rely on unknowable, contingent facts such as these for its defence is
in serious difficulty, especially if one has, as Evans did, anti-realist
inclinations.
[53] Another line of criticism against (2') is that it gets
the modal properties of "Julius" wrong (thanks to Michael Morris for this
objection). If there were just three available referents, (2') would
get what we might call the extensional aspects of "Julius" correct, but
it, unlike (2), fails to capture what these aspects of "Julius" would be
if the referential domain were different (larger, say). But in that
case, it just seems that there are two kinds of descriptive names:
ones for which the referential domain is taken to be fixed, and which has
nothing to say about possible, counterfactual additions to it ("modally
modest" descriptive names), and ones which do have application to
these counterfactual cases ("modally ambitions" descriptive names).
Even if axioms along the lines of (2') cannot capture modally ambitious
descriptive names, they can capture modally modest ones. The upshot
of (2'), then, is not that it shows proper names to be non-Russellian,
but that it shows modally modest descriptive names to be Russellian.
So Evans' conclusions concerning "Julius" cannot be taken to be true of
descriptive names in general. This would be a weak point against
Evans, since his main intention in this area was, arguably, to establish
the possibility of a referring expression being non-Russellian, and this
would still have been accomplished even if there are descriptive names
which are Russellian. For an effective case against Evans, then,
one must look to the arguments given in the preceding sections.
Acknowledgements
[54] Thanks to Mike Martin and the erstwhile members of the
Wolfson Philosophy Society, Oxford for comments on the original
paper. The paper also benefited from two presentations to the
E-Intentionality research group at the University of Sussex; in
particular, comments from Tom Beament, Joe Faith and Manuel de
Pinedo Garcia were helpful. Thanks also to Adrian Cussins,
Michael Morris and Murali Ramachandran.
School of Cognitive & Computing Sciences
University of Sussex
ronc@cogs.susx.ac.uk
http://www.cogs.susx.ac.uk/users/ronc
References
Carruthers, P. (1987) "Russellian Thoughts". Mind XCVI, No 381: 18-35.
Dancy, J. (ed.) (1988) Perceptual Knowledge. Oxford: Oxford University Press.
Davidson, D. (1967) "Truth and Meaning". Synthese 17: 304-23.
Davidson, D. and G. Harman (eds.) (1972) Semantics of Natural Languages. Dordrecht: Reidel.
Dummett, M. (1973) Frege: Philosophy of Language. London: Duckworth.
Evans, G. (1982) The Varieties of Reference. J. McDowell (ed.). Oxford: Clarendon Press.
Jackson, F. (1998) "Reference and Description Revisited", http://coombs.anu.edu.au/Depts/RSSS/Philosophy/People/Jackson/ref.html, accessed on November 26th, 1998.
Kripke, S. (1972) "Naming and Necessity". In Semantics of Natural Languages, D. Davidson and G. Harman (eds.). Dordrecht: Reidel.
McCulloch, G. (1985) "A Variety of Reference?" Mind XCIV.
----- (1989) The Game of the Name. Oxford: Clarendon Press.
McDowell, J. (1977) "On the Sense and Reference of a Proper Name". Mind LXXXVI.
----- (1982) "Criteria, Defeasibility and Knowledge". Proceedings of the British Academy LXVIII: 455-479; reprinted with additions and revisions in Dancy (1988).
----- (1987) "In Defense of Modesty". In Taylor (1987).
Peacocke, C. (1981) "Demonstrative Thought and Psychological Explanation". Synthese XLIX: 187-217.
Taylor, B. (ed.) (1987) Michael Dummett: Contributions to Philosophy. Dordrecht: Nijhoff.
Notes
1 Although discussion of
such reference-fixing stipulations for names was discussed
earlier, as Evans pointed out, by Kripke in "Naming and
Necessity" (Kripke 1972: 290-1). (back)
2 A precedent for this
way of finessing simplistic externalist objections to Fregean
theory can be found in the account of the senses of
demonstratives and indexicals in Peacocke's "Demonstrative
Thought and Psychological Explanation". (back)
3 I use the qualification
"reasonable" since there are, strictly speaking, other options,
such as insisting that only referring expressions have sense,
that are not worth considering. (back)
4 Compare the disjunctive
account of perception in (McDowell 1982). (back)
5 One might think that
{F1} is not needed; holism can be rejected because it is
incompatible with the Generality Constraint (VOR, page
100), in that holism will imply that it is not the same sense,
and thus not the same ability, involved in understanding the
sentences "John is happy" and "Harry is happy", when "Harry", but
not "John", is empty (thanks to Tom Beament for raising this
point). This is indeed a consequence of the holism which {F1} is
meant to prevent, but it does not violate the Generality
Constraint. As we are about to see, Evans makes a distinction
between what is thought and what is said; the Generality
Constraint applies directly to the former, and only derivatively
to the latter. The holist is free to maintain that even though a
subject grasps different senses when understanding the two
sentences, those senses may, indeed must, respect the Generality
Constraint. Possessing the ability to think the thought expressed
by "John is happy" implies the possession of abilities involved
in thinking the thoughts expressed by "Fred is happy" (assuming
"Fred" is not empty) and "John is old"; similarly, possessing the
ability to think the thought expressed by "Harry is happy" when
"Harry" is empty implies the possession of an ability involved in
thinking the thought expressed by "Alice is happy" (assuming
"Alice" is empty), etc. (back)
6 An earlier version of
this paper, "The Significance of Singular Terms: A Critique of
Evans", presented to the Wolfson Philosophy Society, Oxford, 1
May 1990. (back)
7 The "^" indicates
concatenation. Evans used the underline to indicate uniqueness;
the short vertical stroke indicates the unique variable when more
than one variable is present. There are two technical details
concerning this axiom as printed in VOR that only warrant
mention in a footnote. First, on the left hand side of the
equation "f" is a schematic variable
ranging over expressions, since it is to be replaced with
something which can be concatenated with an expression. Yet on
the right hand side "f" ranges over
properties, since it is to be replaced with something for which
the question of satisfaction arises. One way of reformulating the
axiom to rectify this is to do so in terms of what we might call
"M-satisfaction": an object x M-satisfies an expression f iff x satisfies the property denoted by
f. The axiom is then as before, with
"M-satisfies" in place of "Satisfies". Perhaps Evans had some
such non-standard notion of satisfaction in mind; this would
explain the non-standard capitalisation of "Satisfies". Second,
there is a minor mismatch between the use of the underscoring
notation used in stating (14) on page 53 with that used in
stating (8) on page 36; it seems most likely that the latter
should be emended to resemble the former, but to avoid confusion,
I have reproduced (14) unmodified, and have used the same
notation for clause {N} in what follows. (back)
8 Although Evans did, of
course, agree with and argue for the conclusion that definite
descriptions, as Russell argued, should not be seen as referring
expressions but instead be given a quantificational account. That
he does so makes his classification of descriptive names as
referring expressions rather contentious, even sixteen years on;
witness Jackson: "...[O]ne who insists that definite descriptions
are not referring expressions on the basis of a Russellian story
about them, is committed to saying that rigidified definite
descriptions are not referring expressions either" (Jackson 1998). (back)
9 And also because we
need to show how the reference of definite descriptions "depends
upon the significance of the words embedded in the description".
But unless shown otherwise, I'll assume that the existence of
this other motivation makes no impact on my arguments. (back)
10 Simplicity seems to
have been a relevant consideration for Evans in this matter. For
example, he eventually rejects (14) as an account of definite
descriptions on the grounds that in order for it to account for
our all of our ways of using definite descriptions, we must
relativise the notion of reference to a possible world. Although
he states that this is unacceptable because this "would allow
[names, pronouns and demonstratives] to get up to tricks they
never in fact get up to", this could be remedied by proposing
that it is only the reference of definite descriptions that is
relative to a possible world, while the reference of names
remains unrelativised (compare Jackson, op cit.). This
inelegant idea, I take it, was not considered as a solution
because of its complexity, in proposing two kinds of reference,
when compared to the simplicity of a quantifier-based treatment.
Incidentally, I take it that Evans' ultimate rejection of (14) in
favour of a quantifier-based account does not diminish the
interest in the reasons he gave for preferring (14) over (13),
and the difficulty with which those reasons are integrated with
his views on proper names and definite descriptions. (back)
11 If this stipulation
seems a little too bizarre to have anything to do with actual
language use, consider the naming of monarchs ("Let us call the
nth monarch named X 'King'^X^n when male, 'Queen'^X^n when
female") or the naming of stars ("Let us call the nth star in the
constellation X, Xn"). As McCulloch points out, this
needs to be restricted to those cases where we only have
the description to fix the referent, and not, say, a
demonstrative means of identification in addition (McCulloch
1989: 289-90), but this does not affect the point being made. For
the difference between "satisfies" and "Satisfies", see endnote
7. (back)
* Editor's note:
Curly brackets indicate that the label of the proposition is the
author's own. Regular parentheses are used when the label is the
one used by Evans. (back)
* Editor's
note: Because present HTML standards rule out proper
representation of some of the logical formulations, we have used
a special notation to indicate Evans' underscoring with raised
marks. In place of the raised mark in the underlining, the
underscoring instead is interrupted, and the relevant variable is
printed in bold. Thus, formula (14) above appears in VOR
as:
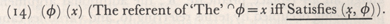
Formula {N} and {2*} above also use this notation. (back)
©1998 Ronald Chrisley
EJAP is a non-profit entity. EJAP may not be printed, forwarded, or otherwise distributed for any reasons other than personal use. Do not post EJAP on public bulletin boards of any kind; use pointers and links instead. EJAP retains the right to continuously print all the articles it accepts, but all other rights return to the author upon publication.
EJAP is hosted at The University of Louisiana at Lafayette. Please send comments and questions to ejap@louisiana.edu.